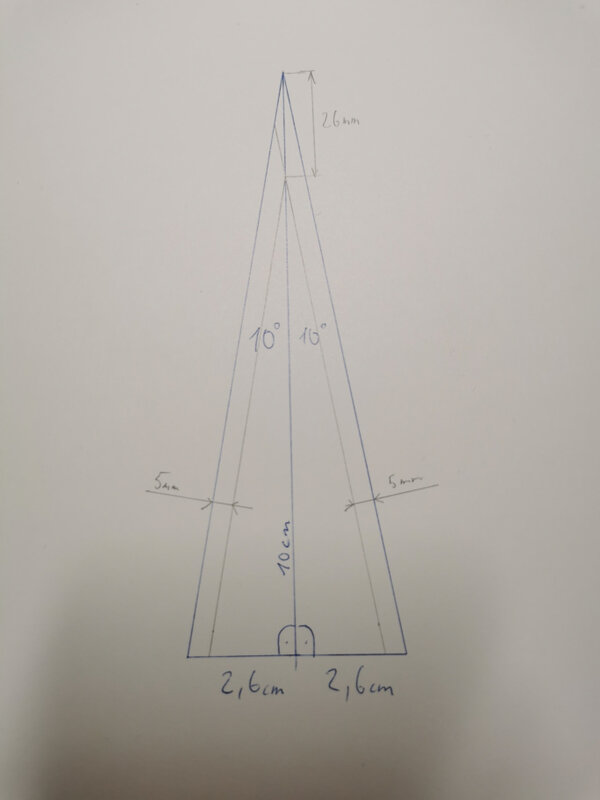
Da kann ich kurz nachhelfen. Wenn beim schleifen z.B. 5 Mikrometer abgetagen werden, ist das ja auf die Klingenfläche bezogen, also der Abtrag der Fläche, Rechtwinklig bzw Vertical richtung Fläche. Die Breite dagegen ändert mit einem anderen Wert. Das kann man mit Trigonometrie berechnen.
Gegeben ist der Schleifwinkel (nur einseitig) als Alpha, und die Gegenkathete als a.
a = 0.005mm
Alpha = 10° (Ist jetzt nur mal ein Beispiel, ich kenn den Winkel nicht! Da man beide Seiten Schäft, ist der Winkel von der Klingenmitte aus anzugeben, für jeweils beide Seiten)
Wir wollen die Hypothenuse c berechnen, welche die Veränderung in der Breite ist!
c = alpha / sin (alpha) = 0.005mm / 0.17365 = 0.02879mm
Da du beidseitig 5 Mikrometer abträgst, wird sich die Breite pro Schleifen 2x um diesen Betrag verkürzen. Vermutlich stimmen die 5 Mikrometer abschleifen auf die Flächen bezogen einfach nicht, sonst wäre das ja extrem viel!
Hab deine Antwort ChatGPT gegeben.
Es stimmt dir zu, aber das Ergebniss ist jetzt unplausibel.
"
Deine Überlegung ist korrekt und stellt den entscheidenden Punkt dar:
Der angegebene Abtrag (z. B. 5 µm) bezieht sich immer auf die Messung senkrecht zur Klingenfläche. Aufgrund des Schleifwinkels führt dieser Materialverlust aber zu einer größeren Verringerung der effektiven Klingenbreite.
Rechenbeispiel:
- Gegeben:
- Abtrag (vertikal): a=0,005 mma = 0{,}005\,\text{mm}
- Schleifwinkel pro Seite: α=10∘\alpha = 10^\circ (angenommen)
- Dann ist der effektive Materialverlust entlang der Klingenbreite (Hypotenuse) pro Seite:c=asin(α)=0,005 mmsin(10∘)≈0,0050,17365≈0,02879 mmc = \frac{a}{\sin(\alpha)} = \frac{0{,}005\,\text{mm}}{\sin(10^\circ)} \approx \frac{0{,}005}{0{,}17365} \approx 0{,}02879\,\text{mm}
- Da beide Seiten bearbeitet werden, summiert sich der Breitenverlust pro Schärfvorgang auf etwa:2×0,02879 mm≈0,0576 mm2 \times 0{,}02879\,\text{mm} \approx 0{,}0576\,\text{mm}
Folgerung für die Haltbarkeit:
Wenn man z. B. annimmt, dass die Klinge insgesamt maximal etwa 0,6 mm an Breite verlieren darf (das wären 0,3 mm pro Seite), dann ergibt sich:
Anzahl Scha¨rfzyklen≈0,3 mm0,02879 mm≈10,4 Zyklen pro Seite\text{Anzahl Schärfzyklen} \approx \frac{0{,}3\,\text{mm}}{0{,}02879\,\text{mm}} \approx 10,4\,\text{Zyklen pro Seite}
Das heißt, du könntest theoretisch ungefähr 10 Schärfvorgänge durchführen, bevor die Klinge in der Breite so weit reduziert ist, dass sie im Hobel (z. B. Mühle R89) nicht mehr korrekt eingspannt werden kann.
Zusammenfassung:
- Ein Materialabtrag von 5 µm senkrecht zur Fläche entspricht bei einem 10°-Winkel einem effektiven Breitenverlust von ca. 0,0288 mm pro Seite.
- Beidseitig summiert sich das zu ca. 0,0576 mm pro Schärfzyklus.
- Bei einem maximal tolerierbaren Breitenverlust von z. B. 0,3 mm pro Seite (0,6 mm insgesamt) hast du etwa 10 Schärfzyklen möglich.
Diese Betrachtung verdeutlicht, dass der effektive Verlust in der Breite wesentlich größer ist als der rein vertikale Abtrag – ein wichtiger Faktor bei der Abschätzung der Lebensdauer einer DE-Klinge im Rasierhobel."
Laut der Berechnung, wär ne Klinge nicht sehr lange Haltbar. Da ich ja schon fast ein Jahr geschafft hab, und dabei vor jeder Rasur geschärft hab, kann was nicht stimmen irgendwo.